The Queue Layout Problem
A queue layout of a graph consists of a linear order of its vertices, and a partition of its edges into queues, such that no two edges in the same queue are nested .
Edge (u,v),
(x,y) nest if 
.
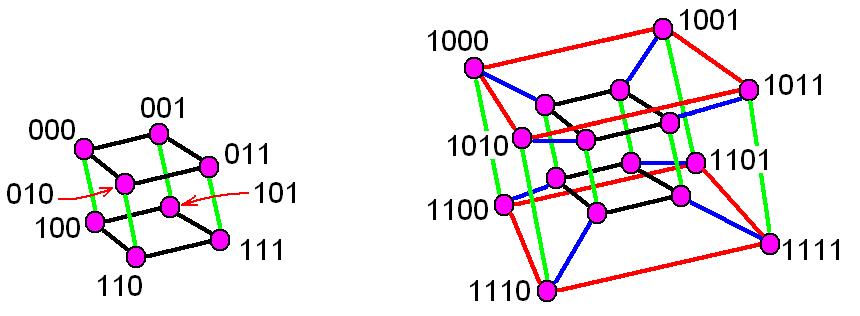
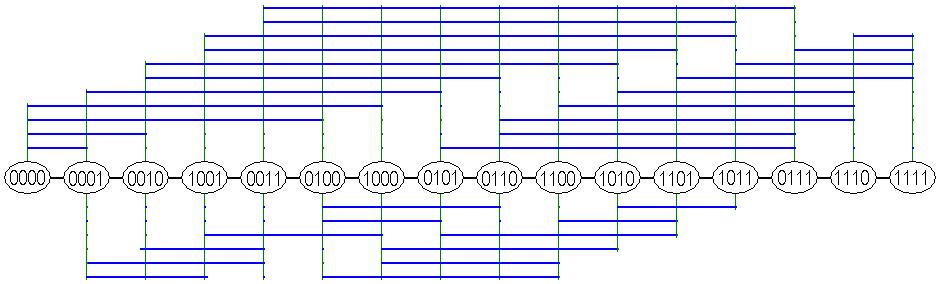
For example: A 2-queu layout of Hypercube Q4 is shown as below:
The Power Domination Problem
The power
domination problem is to find a minimum
placement of
phase measurement units (PMUs) for observing the whole
electric power system, which is closely related to the
classical domination problem in graphs. For a graph
G(V,E), the power domination number of G is the minimum
cardinality of a set S 
V such that PMUs placed on every
vertex of S results in all of V being observed. A vertex
with a PMU observes itself and all its
neighbors,
and if an observed vertex with degree d
> 1 has only one
unobserved neighbor, then the unobserved neighbor becomes observed.
Observation
Rule 1 :
A PMU on a vertex v observes v and
all its neighbors.
Observation Rule 2 :
If an observed vertex u with
degree d > 1 has only one unobserved neighbor v, then
v becomes observed as well.
The k-Rainbow Domination Problem
Let f be a
funtion that assigns to each vertex a set of colors chosen from the set {1, ... ,
k}; that is,
f: V(G) 
p({1, ... , k}). If for each vertex v 
V(G) such
that f(v) = 
we have 
f(u) = {1, ... , k}, then f is
called a k-rainbow domination function ( kRDF ) of G.